这里我来进一步分析阿杰的所谓的作图求两个零点的方法是多么荒唐可笑。
我里我想说明一点。我为什么要用12吋臂来作为例子呢?这是因为他所有图都是以12吋臂为基础的。我用来计算及作图的臂为,有效长度为304.8mm,超距为13.4mm,补偿角为17.8度。这是个很标准和基本的12吋臂。

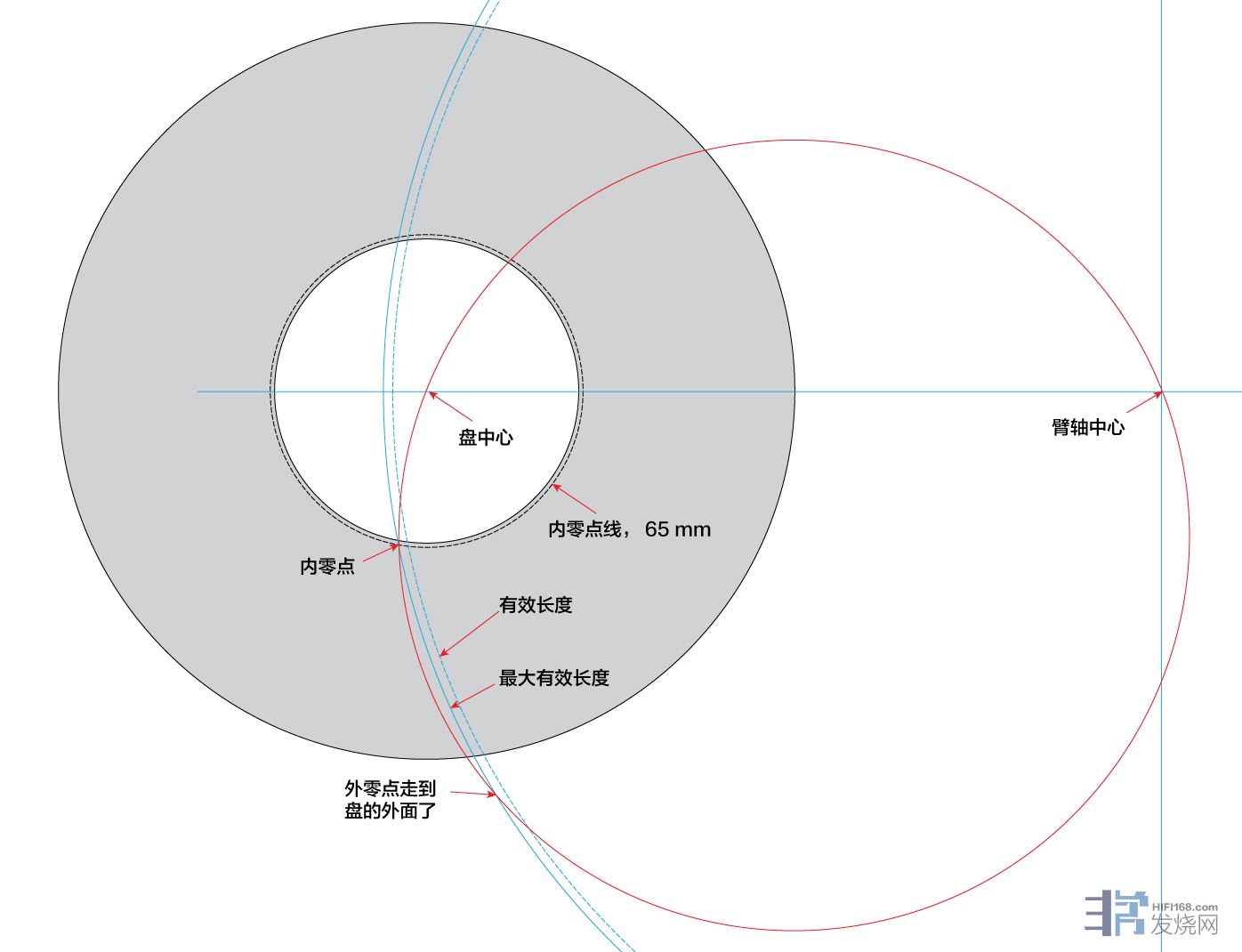
现在我完全按他的逻辑来推论。图中蓝色线是针的轨迹。蓝色的虚线是臂原始设计的轨迹。但他自认为发现了新大陆,他说最大有效长度。他又说最大有效长度下误差最小。他的最大有效长度说白就是让针达到最前端。我这里取4mm。这时臂的轨迹就走在蓝线上了。他又取了一个红色圆形,这个圆形和盘中心,臂轴中心及内零点相交。按照他的讲法,这圆和蓝色轨迹相交的两点就是两个零点。在图中,我们可以看到,其中一个零点存在,另外一个零点走出了盘最外圈。这完完全全是荒谬的。
这里可以看出他整一套推论的过程及结果都是荒谬的。LP中计算零点及平均误差的理论及方法是非常成熟的,根本不需要任何人来发明什么。更不需要象他那水平低下的来胡诌!